自分用メモ

プログラミングとかのメモを書きたいです

無償版G Suiteの終了の対応について[検討]

背景

  • 無償版G Suite(Google Workspace、旧Google Appsl for your domain)が有償化する。
  • このままだと独自ドメインのメールが使えなくなってしまうので、対応を検討。

【追記】 案4を採用した。 とりあえずメール受信はできたのでいったんOKかと思う。 ただし、そのうち、ちゃんとドメイン管理的なことをしたいような気もする。

現在の環境

  • G Suiteをhoge@xxx.comで使っている。ただし、使っているのはメールのみ。 しかも、hoge@xxx.comに届いたメールは個人Gmail(hoge@gmail.com)に転送しているだけ。
  • 独自ドメイン(xxx.com)はValue-domainで契約して、value-domainのDNS設定を使っている。value-domainにはMXレコードなどの設定が入れてあり、それでG Suiteと連携している
  • 一人で使っているだけなので、アカウントは1個でOK

変更案

今の所結論はでていない。案4を試しておいて、案1か案2,3かなぁ。

案1：Google Workspace

現状から変化が一番少ないパターン。カネで解決。

  • Business Starter(680円/月)： ストレージは30GB
  • Business Standard(1,360円/月)：ストレージは2TB

案2：MS365(Business)

MSに切り替え。現在はMS365(Personal)に入っているので、こちらに統合すると費用増は少なめになる。 MSアカウントが1つのメルアドに対して、個人用とビジネス用と2種類になってしまい、ややこしくなりそう。(メールはOfficeはビジネスだし、それ以外は個人用)

  • Business Basic(540円/月)：ストレージ1TB、デスクトップ版Officeアプリはなし(Web/モバイルはあり)
  • Business Standard(1,360円/月)：Officeアプリがつく

案3：MS365(Personal)＋GoDaddy

最終的にはシンプルだけど、Value-DomainからGoDaddyへの切り替えが必要なのはめんどい。

  • Personal(1,284円/月)：家庭向け(独自ドメインのメールを使うには、GoDaddy(年間2000円、Value-Domainは年間1500円)への切り替えが必要なもよう)

案4：Value-domainの機能で個人Gmailにメール転送だけする

  • お金がかからないし、これが一番現実的かも。

案5：Value-domainかなにかでメールサーバを用意する

  • xreaMail&Backup：安いけどメールサーバは大手のほうが安心感ある
  • Amazon Workmail($4/月)：大手ではあるけど、これを使うならGoogleかMSがよいかも。

AWSで価格取得してLineBotに送る

やったこと

  • AWSの価格を取得して、定期的にLineで配信する
  • 言語はPython。
  • 概要図は下記
    • なお、本記事でぜんぶ網羅して説明できていなくて、上から順にやっても手順漏れまくりなことに注意。ポイントっぽい部分のメモでしかないです。

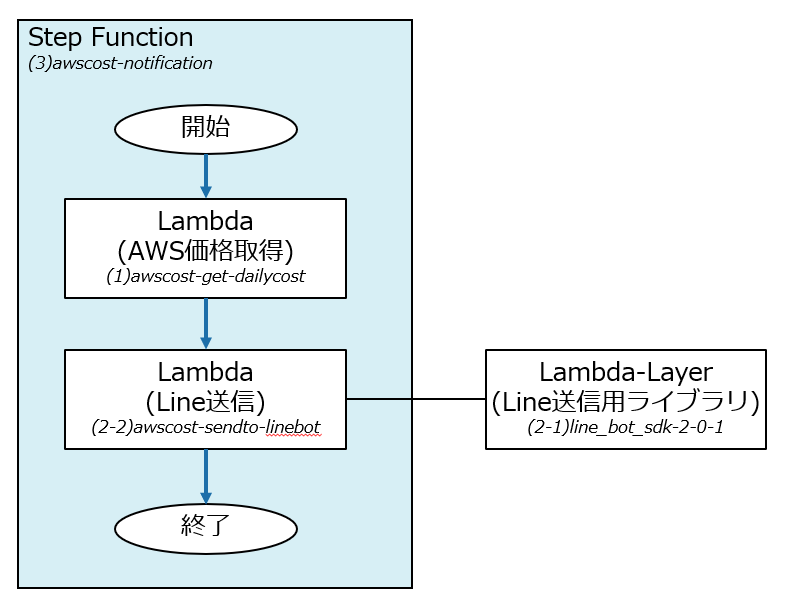
f:id:ebinafactory:20211123223009p:plain
概要

Lineに投稿される内容

f:id:ebinafactory:20211123233643p:plain

背景

  • AWSをいろいろ触ってみる間に、AWS価格を配信してくれる仕組みが欲しくなった。
    • メール配信よりも、Lineに投げてみたい
  • AWSそのものの勉強もしたかった。
    • Lambda や その周辺の権限など

概要

  • (1) LambdaでAWSの価格取得する関数を作成
  • (2-1) LambdaのLayerでlinebot用のPythonライブラリのLayerを用意した
    • Layerというのは、Lambda用のライブラリセット。Lambda本体に同梱しても良いはずだけど、Line送信するライブラリは将来作成した別のBotでも使いそうな気がしたので、Layer化してみた
  • (2-2) LambdaからLineに対してメッセージ送信。
    • 自分しか使っていないLineBotアカウントからブロードキャスト送信する形とした。(自分のLineのuseridがわかればToでできそうだったけど、自分のLineのuseridがわからなかった・・・。)

  • (3) これらをまとめるStepFunctionを作成

    • このStepFunctionを定期実行するようにした

  • その他メモ

    • 権限は結構ややこしかった。上手な設計や運用方法はまだつかめていない上にたぶん漏れがあるけど、記憶の範囲で記載する。
      • Lambdaなどは、設定したIAMロールで動くことになる。このIAMロールにはLambdaを実行するための権限であったり、ログ出力(CloudWatch Logs)に書き込むための権限が必要になる。今回、コスト参照を行っているため、CostExplorer関係の権限を付与した。
    • boto3
      • PythonからAPIを実行するときの公式ライブラリ。lambda環境はデフォルトでインストール済みであり公式サンプルもこれ。
        • lambda環境からの実行：lambda実行ユーザとして動ける(ソース内にIAMユーザのトークンなどは不要)
        • ローカル環境からの実行：IAMユーザのトークンなどを使って使う(IAMユーザに権限付与も必要)
    • ソースとトークン(パスワード的な文字列)の分離
      • Lambdaには環境変数がセットできる。パスワードは環境変数にセットして、ソースは環境変数からパスワードを取得するようにするのが定番の方法。

手順

(1)LamndaでAWS価格の取得

  • 環境メモ
  • 開発時のメモ
    • VSCodeなどでローカル開発したほうがやりやすい。その際、boto3のclientは下記のように情報を追加すれば、ローカルからもつながる。
    • IAMユーザのシークレットアクセスキーは、IAMユーザ作成時にしか出てこないのでちゃんとメモする。(メモしそこねたらリセットができる)
client = boto3.client('ce',
    aws_access_key_id='IAMユーザのアクセスキーを入れる',
    aws_secret_access_key='IAMユーザのシークレットアクセスキーを入れる',
    region_name='us-east-1'
)

from datetime import datetime, timedelta, date
import boto3
import json

# 今日-start ～ 今日+end日前までのコストを求める
def get_cost_for_oneday(client, start, end):
    # 日付を計算
    start_date = date.today() - timedelta(days=start)
    end_date = date.today() + timedelta(days=end)
    # API用に文字列にする
    start_str = start_date.strftime('%Y-%m-%d')
    end_str = end_date.strftime('%Y-%m-%d')
    # APIを実行する
    response = client.get_cost_and_usage(
        TimePeriod={
            'Start': start_str,
            'End': end_str
        },
        Granularity='DAILY',
        Metrics=[
            'AmortizedCost'
        ]
    )
    # Metricsの参考。
    # https://qiita.com/tamura_CD/items/4a9a412faf379b334986

    # responseはdictで、['ResultsByTime']に各日付の情報が入っている
    ret_list = []
    for d in response['ResultsByTime']:
        tmp = {
            'start' : d['TimePeriod']['Start'],
            'end' : d['TimePeriod']['End'],
            'billing' :  d['Total']['AmortizedCost']['Amount']
        }
        ret_list.append(tmp)
    return ret_list


def lambda_handler(event, context):
    # boto3で接続
    client = boto3.client('ce', region_name='us-east-1')
    # 3日前～今日を取得する
    ret = get_cost_for_oneday(client, 3,0)
    return {
        'statusCode': 200,
        'body': ret
    }

(2-1)LambdaのLayer(Line送信用ライブラリ)

(2-2)LambdaのLine送信

  • ソースは下記
  • Layerに(2-1)で作ったものを指定する。
  • 環境変数にLineのアクセストークンを入れる必要がある。(これを見つけるのに結構はまった。後術。)

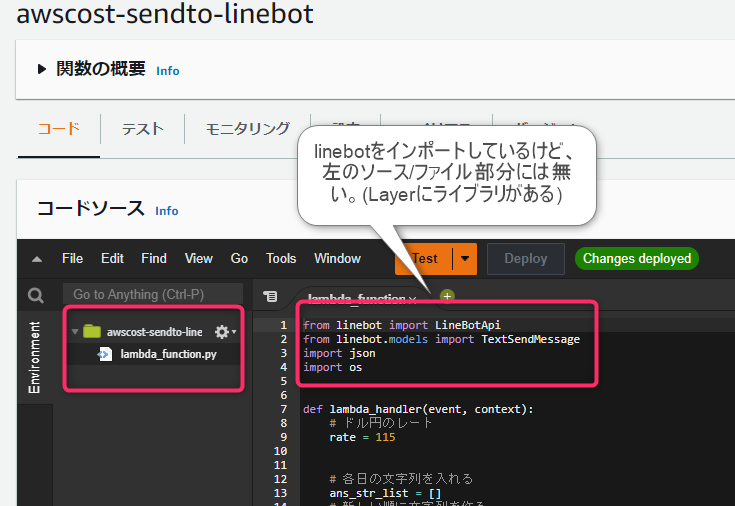
f:id:ebinafactory:20211123231147p:plain

from linebot import LineBotApi
from linebot.models import TextSendMessage
import json
import os


def lambda_handler(event, context):
    # ドル円のレート
    rate = 115

    
    # 各日の文字列を入れる
    ans_str_list = []
    # 新しい順に文字列を作る
    costdata_list = reversed(event['body'])
    for d in costdata_list:
        doller, start, end = d['billing'], d['start'], d['end']
        yen = int(float(doller) * rate)
        tmp = f'{yen}円： 期間[{start}～{end}], (${doller})'
        ans_str_list.append(tmp)
        # print(tmp)

    mes_text = "\n".join(ans_str_list)
    #print(mes_text)

    messages = TextSendMessage(text=mes_text)

    # 環境変数でセットする(Line DevelopersのMessagingAPIのChannel access token (long-lived))
    CHANNEL_ACCESS_TOKEN = os.getenv('CHANNEL_ACCESS_TOKEN')
    line_bot_api = LineBotApi(CHANNEL_ACCESS_TOKEN)

    

    # Lineにメッセージを投げる
    line_bot_api.broadcast(messages)
    
    return {
        'statusCode': 200,
        'body': json.dumps('Hello from Lambda!')
    }

(2-2)Line developers

正直良くわかっていないけど、いくつかわかったこと。 * Line Developerに登録する。チャンネルを作るとBot用のアカウントが作成されるような形になる。APIからはこのアカウントが操作できる感じ。Bot用アカウントと個人Lineアカウントを友だち状態にしておいて、ブロードキャスト送信するかたちとした。(ピンポイントで送信する方法がよくわからなかったので) * PythonでLine botを作ってみた - Qiita * CHANNEL_ACCESS_TOKEN は、LINE Developers の MessagingAPIの画面の一番したのほうにある、Channel access token(long-lived)の値を使う * Lineのuseridはスルッとは分からないようだった(Lineアプリから見えているものとは別のuseridが内部にあり、APIなどからはそのuseridを使う)。個人のuseridがわかれば、broadcastではなく、ピンポイントなメッセージ送信に切り替えられるのに・・・。

(3)StepFunction

  • StepFunctionは、Lambdaを複数つなげたもの。JP1/AJSみたいな感じ。
  • 先に動いたLambdaの戻り値を、後続のLambdaが受け取ることができる。
    • 今回は、1つ目はAWS価格を返すようにして、2つ目はそれを受け取ってLineに投げる作りとした。2つ目を単体でテスト実行するときは、実行時のパラメータにダミーデータを入れることができる。
  • StepFunctionが動くときのロールも注意が必要
    • Lambdaを実行する権限があればOKだけど、Lambda(リソース)に対して実行できるかの権限までちゃんと指定しなければいけない。

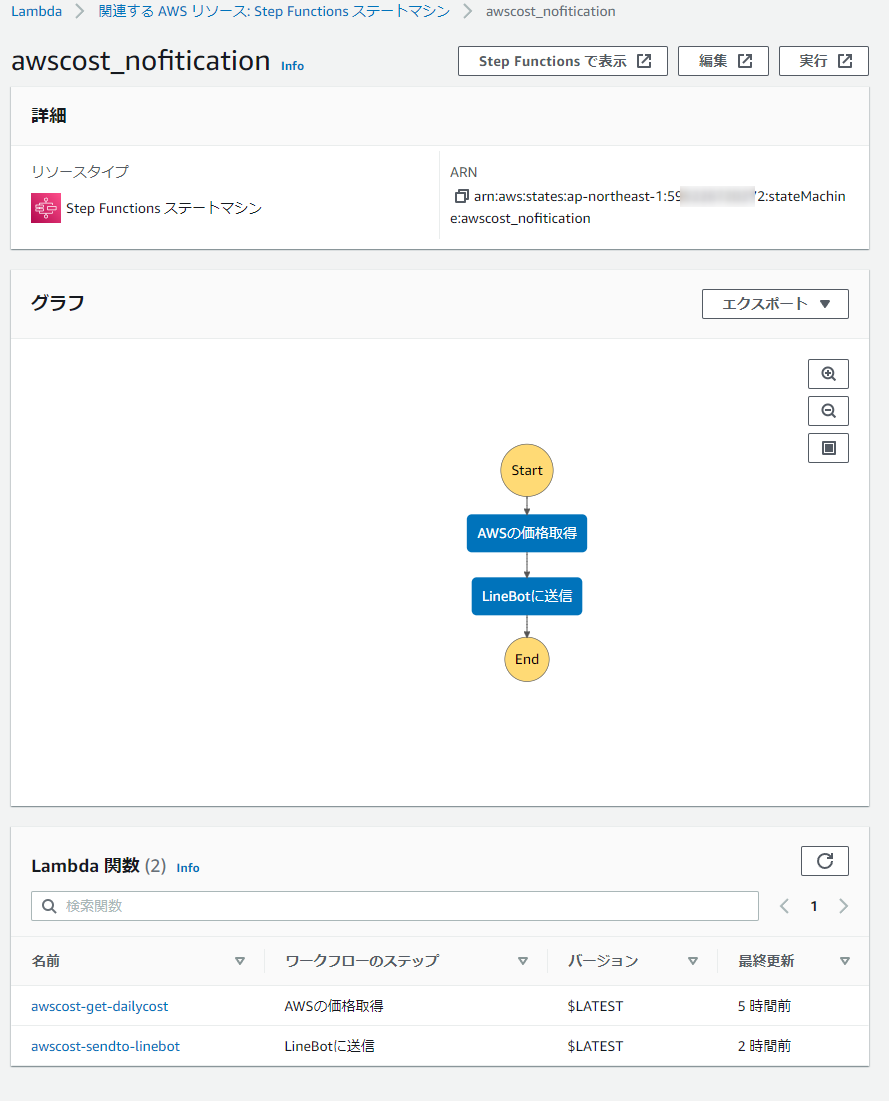
f:id:ebinafactory:20211123233904p:plain

EventBridgeでの定期実行。

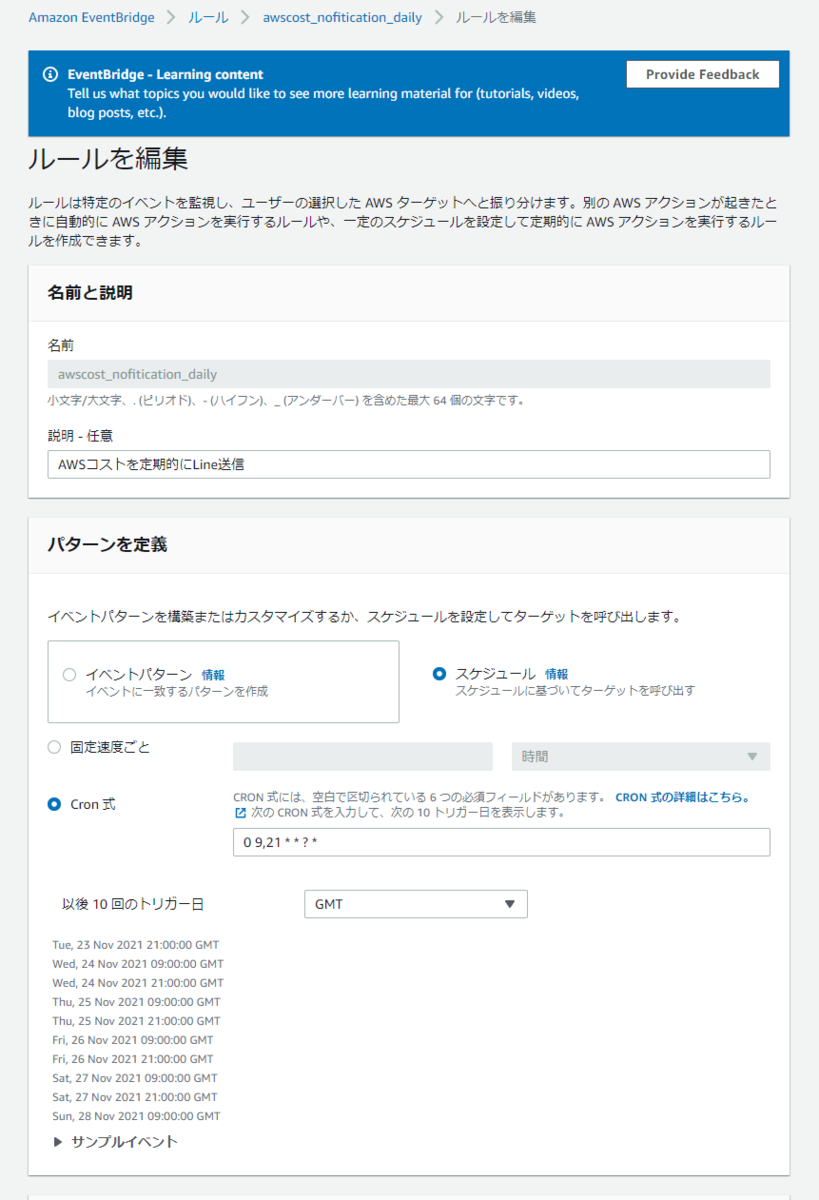
f:id:ebinafactory:20211123233343p:plain

スクリーンショット

AWSのLambdaからSES(Amazon Simple Email Service)を使ってメール送信

AWS lambda

やったこと

  • AWSのLambdaからSES(Amazon Simple Email Service)を使ってメール送信
  • 5分にいちどメール送信

背景

  • AWS料金は、Cost ExplorerのBudgetからアラートを投げることもできるけれど、強制的に定期的に通知するような仕組みが欲しいと思った。
  • 必要そうなことはざっくり下記。
    • lambdaでコードを書いて実行できること(できればpythonで)
    • lambdaで定期実行すること(これはなんか簡単にできそうな印象)
    • lambda でメール送信すること
    • 現在の使用料金の情報を取得すること (今回の対象外)

参考サイト

手順

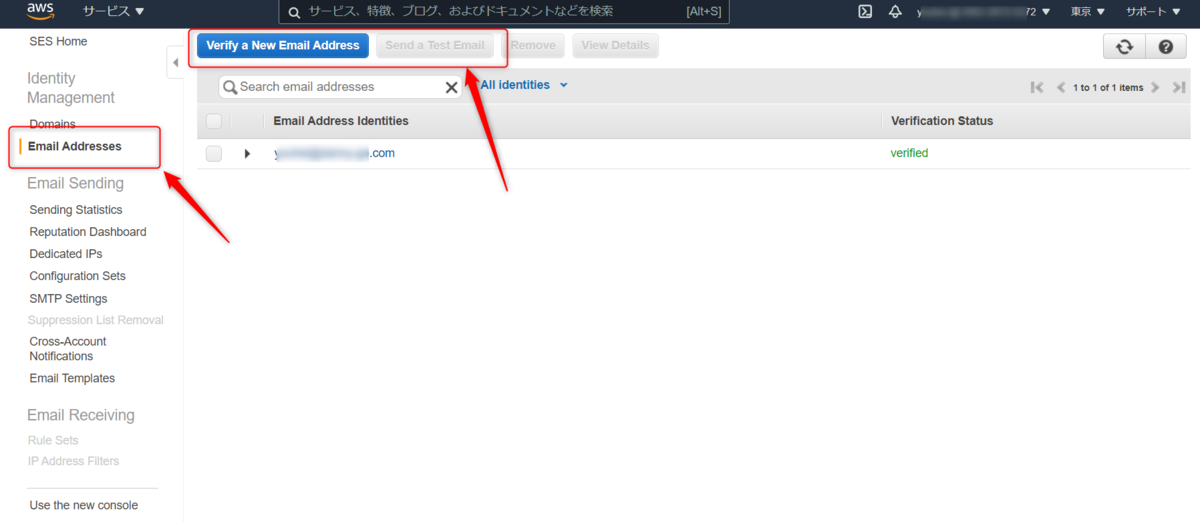
1.SES(Amazon Simple Email Service)の設定

  • 使用するアドレス(送信元にしたいもの)を登録する
  • 詳細は参考URL参照。

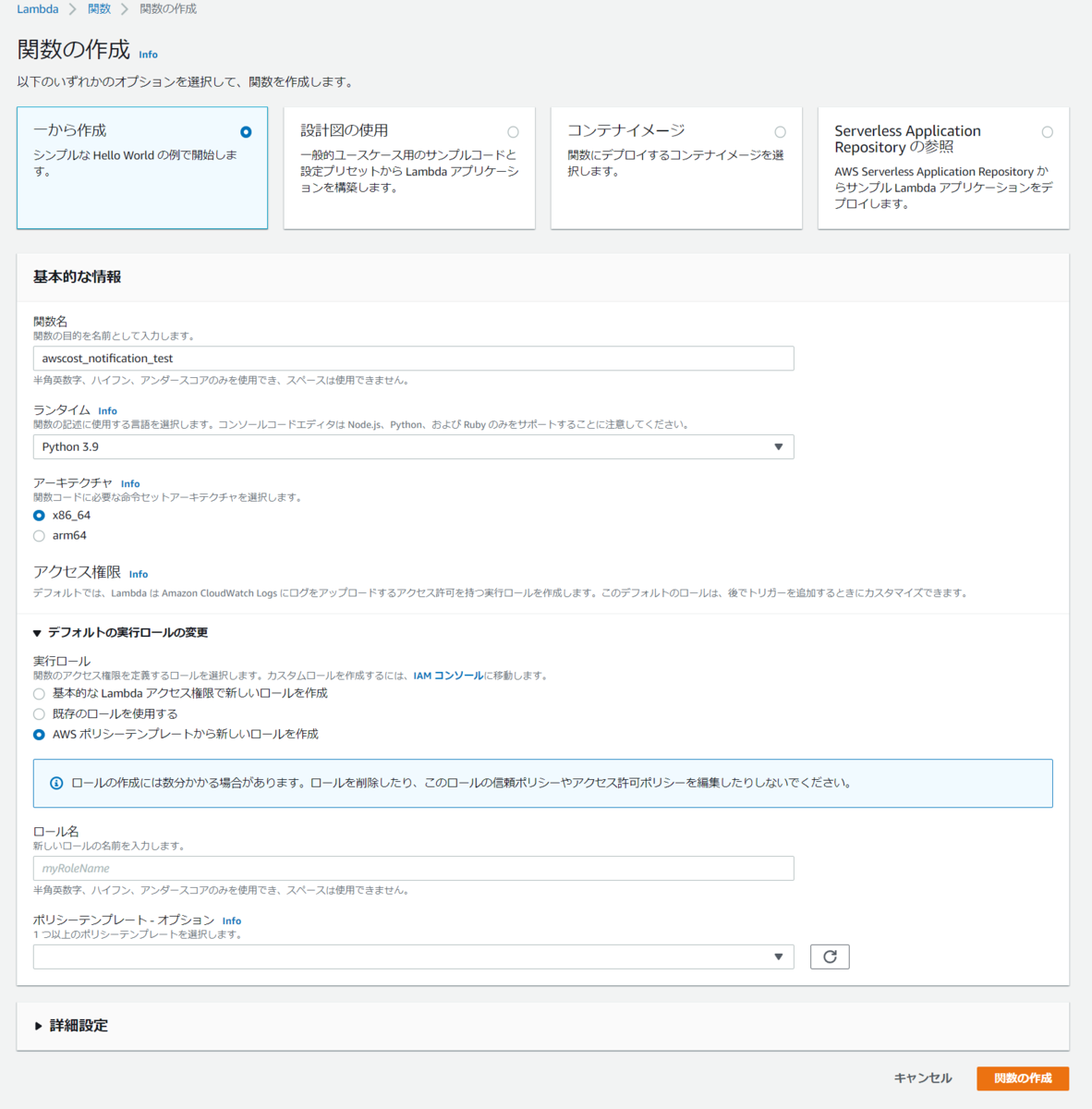
2.関数の定義の作成

  • Pythonで作成する
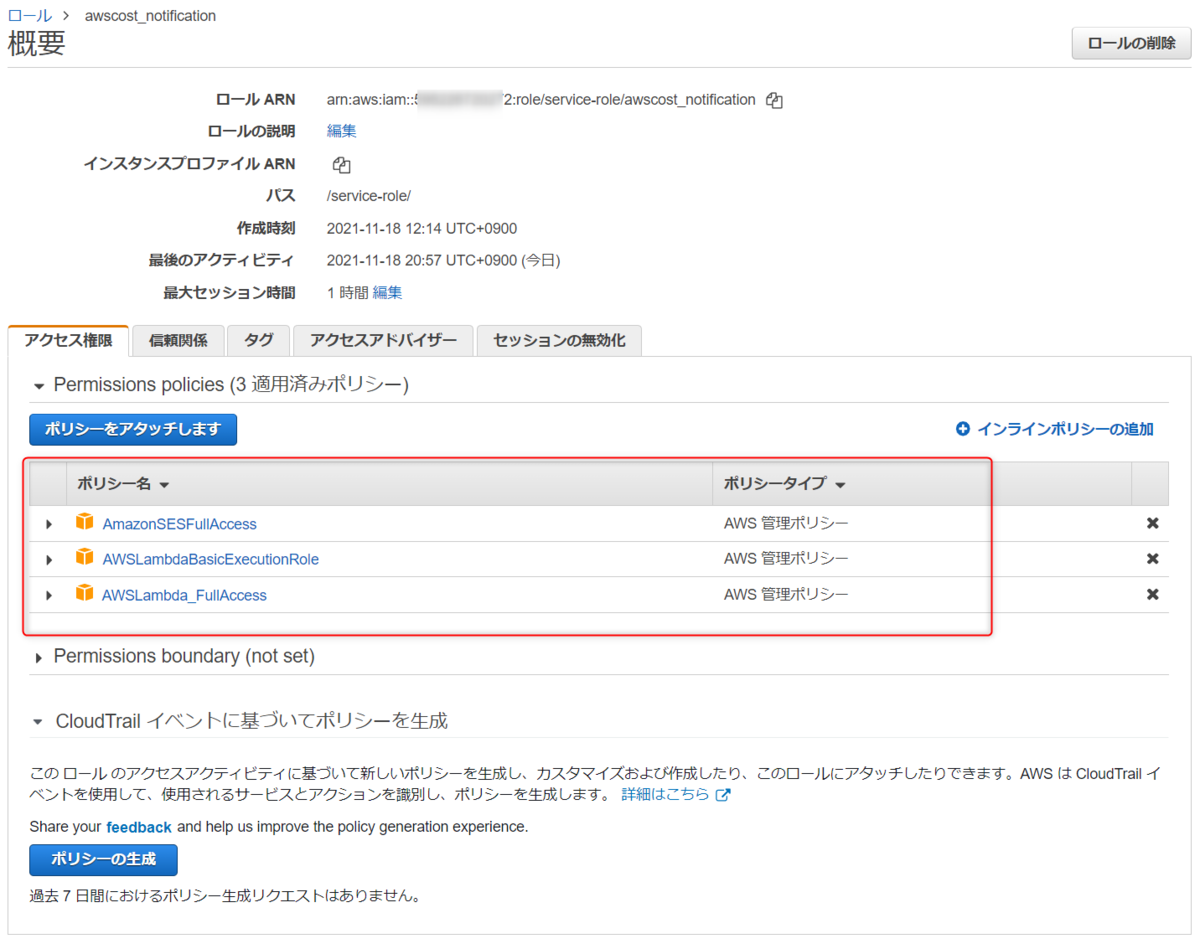
  • ロールは新規に作成してみた。ポリシーは下記の2つとしたが、もっと絞ったほうが良いのかも。
    • AmazonSESFullAccess
    • AWSLambda_FullAccess
    • AWSLambdaBasicExecutionRole
      • これがないと「モニタリング」で「アクセス権限が見つかりません　お使いの関数には、Amazon CloudWatch Logs に書き込むためのアクセス権限がありません。ログを閲覧するには、その実行ロールに AWSLambdaBasicExecutionRole の管理ポリシーを追加します。」と表示される。

3.ソースの記載

  • 参考URLのまま。
import boto3
import json

SRC_MAIL = "送信元のメルアド"
DST_MAIL = "送信先のメルアド"
REGION = "ap-northeast-1"

def send_email(source, to, subject, body):
    print("-- start : send_mail --")
    client = boto3.client('ses', region_name=REGION)

    response = client.send_email(
        Source=source,
        Destination={
            'ToAddresses': [
                to,
            ]
        },
        Message={
            'Subject': {
                'Data': subject,
            },
            'Body': {
                'Text': {
                    'Data': body,
                },
            }
        }
    )
    return response

def lambda_handler(event, context):
    email = "テスト配信"
    message = json.dumps(event, indent = 4)
    r = send_email(SRC_MAIL, DST_MAIL, email, message)
    return r

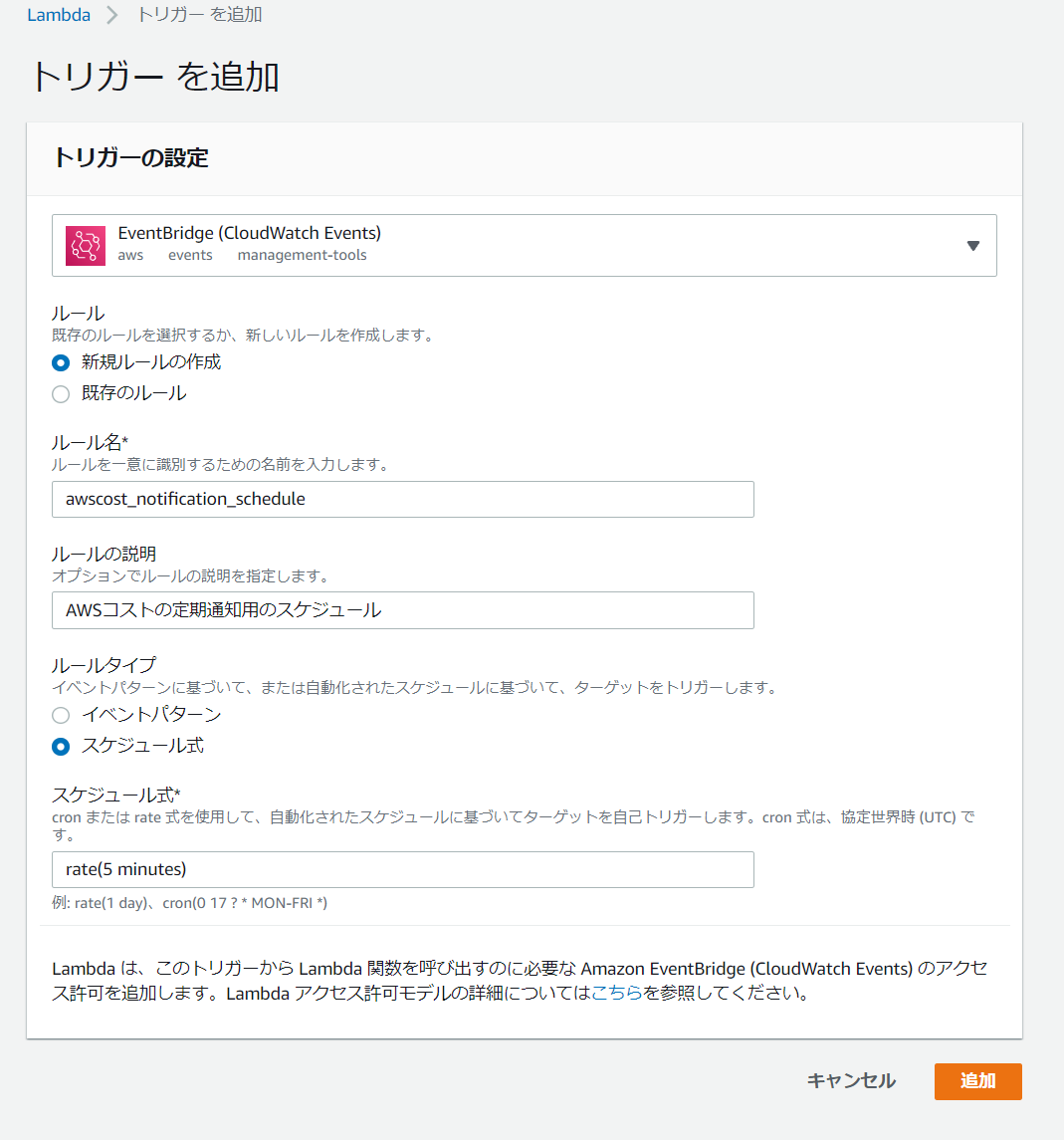
4.定期実行

  • Lambdaのトリガーで、EventBridge(CloudWatch Events)を選択する
  • ルール名、ルールの説明を入れる
  • ルールタイプは「スケジュール式」
  • スケジュール式は「rate(5 minutes)」
    • とりあえず5分おきに実行とする。

参考情報

  • テスト実行する際にはパラメータも渡せる。
  • 標準出力で出しておけば、後でそれが見える。
  • 過去に実行された分もモニタリングで見える

スクリーンショット

f:id:ebinafactory:20211118205932p:plain
AWS Lambda関数の作成

f:id:ebinafactory:20211118213359p:plain
ロール

f:id:ebinafactory:20211118211007p:plain
SES画面。メルアドを登録する。

f:id:ebinafactory:20211118211652p:plain
Lambdaのトリガーで定期実行

Unity(五目並べ)に勝敗表示をつけた＆WebGL出力エラーを直した

Unity
やったこと
実際の手順
  • 勝敗数の保持
    • static変数で黒と白の勝数を保持。static変数なのでどこからでも読める。(マナー的には良くないのかもしれないけど)
  • UIのTextへの表示
    • スクリプトにText型の変数を用意する。コード内ではそのText型の変数に対して変更をかける。
    • GameContoller(GameObject)のInspecterで、Text型の変数がシーン内のUI(Text)であるマッピングをしておく
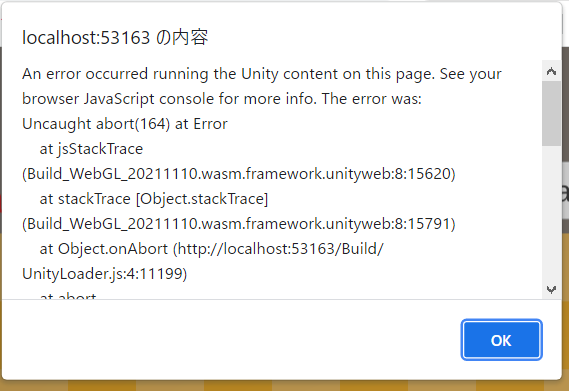
  • WebGLでハマったこと
    • Winアプリとしては表示できるけど、WebGLでは実行時にエラーが出たので、下記で解決した。
      • 音声ファイルが日本語ファイル名だったので、英語に変更した。(関係なかったかも)
      • UpdateやStartの中でText更新(勝数)する際、UI(Text)の変数がnull出ない場合のみとした。
        • 実は実行時のConsoleにエラーが出ており、nullに対して設定していることがわかった。Text型の変数に実態がセットされる前に、StartやUpdateが走るのかもしれない。
覚えておくこと
  • WebGLはエラーが発生しがちだし、エラーメッセージから原因は見つけにくい。
  • エラーが発生するシーンを特定するのが良い。
  • Consoleにエラーが出ていないかを確認する
  • 日本語ファイル名も避けるのが無難
スクショ

f:id:ebinafactory:20211110212040p:plain
キャンバスのText

f:id:ebinafactory:20211110212123p:plain
GameControllerで変数にTextをアサイン

f:id:ebinafactory:20211110212743p:plain
エラー解消したソース

f:id:ebinafactory:20211110214557p:plain
WebGLでの実行時エラー

f:id:ebinafactory:20211110212217p:plain
UI用変数の定義、勝敗数用変数

Unity(五目並べ)にサウンドをつけた

Unity

前回：Unity(五目並べ)にタイトルシーンをつけた - 自分用メモ

やったこと
実装の手順
  • Assetフォルダにサウンド用フォルダを作って、MP3を置く
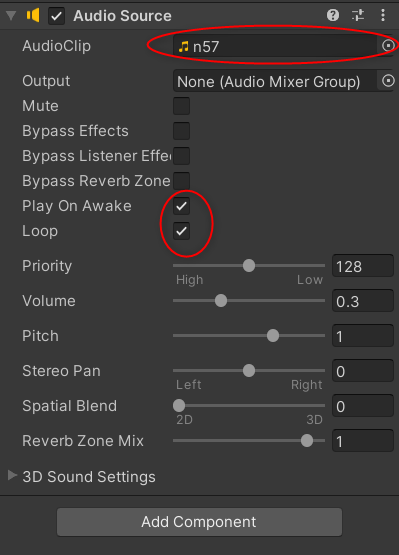
  • GameController(なにかのGameObject)に、Add Componentして、AudioSourceを追加する
  • BGM再生について
    • AutioSourceのOutput にBGM用のファイルを指定
    • 下記をOnにする
      • Play on Awake：開始時に自動再生
      • Loop：ループするかどうか
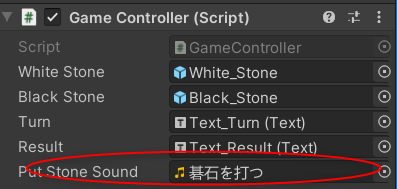
  • 石の音の再生について
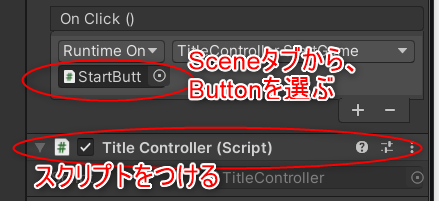
ポイントのスクショ

f:id:ebinafactory:20211109210707p:plain
Assetsフォルダに音用のフォルダを作ってMP3を置く

f:id:ebinafactory:20211109210931p:plain

f:id:ebinafactory:20211109211713p:plain

ソース抜粋
// サウンド
public AudioClip putStoneSound;
AudioSource audioSource;
// コンポーネント取得
audioSource = GetComponent<AudioSource>();
// 石を置く音を鳴らす
audioSource.PlayOneShot(putStoneSound);

Unity(五目並べ)にタイトルシーンをつけた

Unity 技術メモ

Unityの五目並べにタイトルシーンをつけた。

前回：Unity触ってみた(五目並べ) - 自分用メモ

やったこと
  • タイトルのシーンを追加
  • タイトル画面用のスクリプトを追加
    • クリックしたとき用の関数をつける。その関数にはシーン遷移するコードを入れる。
  • タイトルシーンのCanvasにTextとButtonを設置
    • Button にスクリプトをつける
    • Button の OnClickを追加する。 (ここでハマった。Select Objectでスクリプトを選んだりしていた)
      • その際、Select ObjectではSceneのタブから、Buttonを選ぶ
      • [No Function]となっている所から、スクリプトの関数が選べる様になる
参考にしたサイト
スクショメモ

f:id:ebinafactory:20211108235244p:plain

f:id:ebinafactory:20211108235543p:plain
ハマったあたりの画面

AWS：S3にWinSCPでアクセス

AWS
やったことまとめ
  • S3の静的WebサイトホスティングにUnityでつくったWebGLアプリを置いた
    • これはもともと作ってあった。
  • アップロードがめんどくさいので、API用のユーザを作ってWinSCPでアップロードできるようにした
    • 今回の本題。
AWSでやったこと
  1. IAMユーザを作成
    • APIだけにする
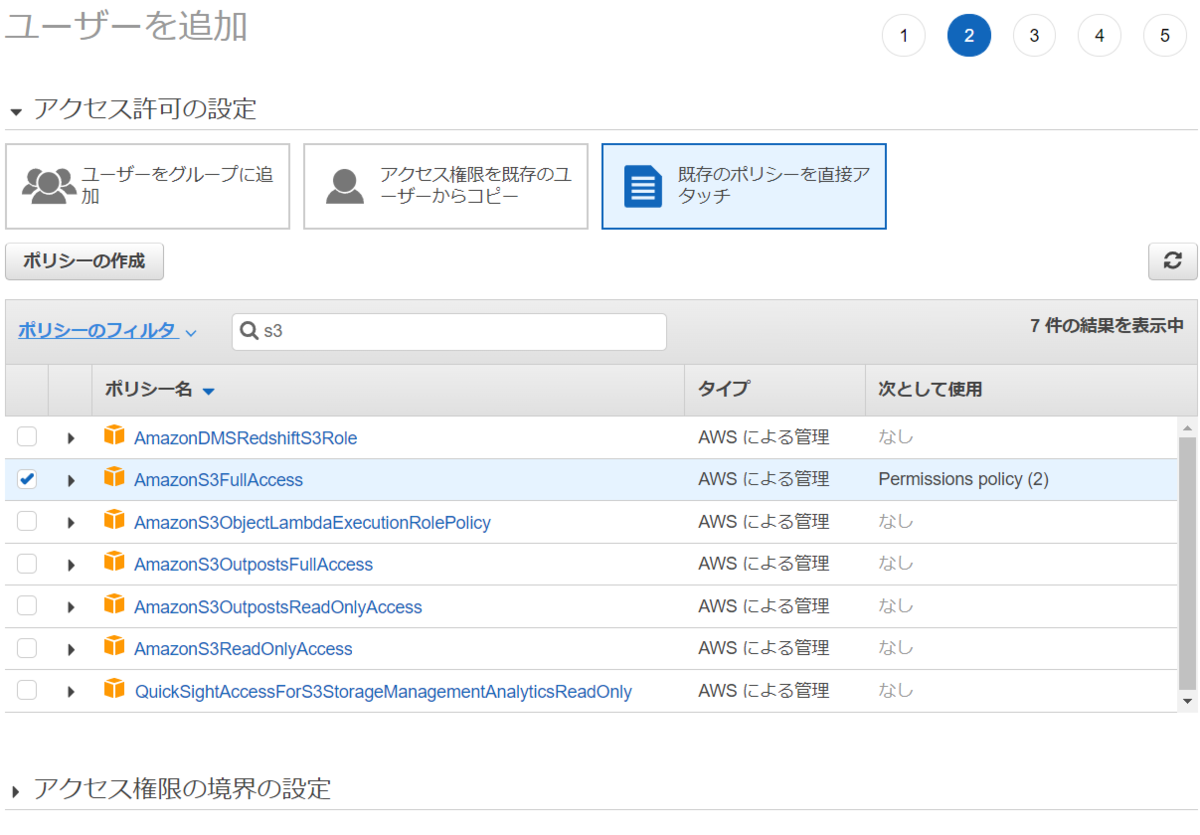
  2. ポリシーをタッチする
    • S3へのアクセス権
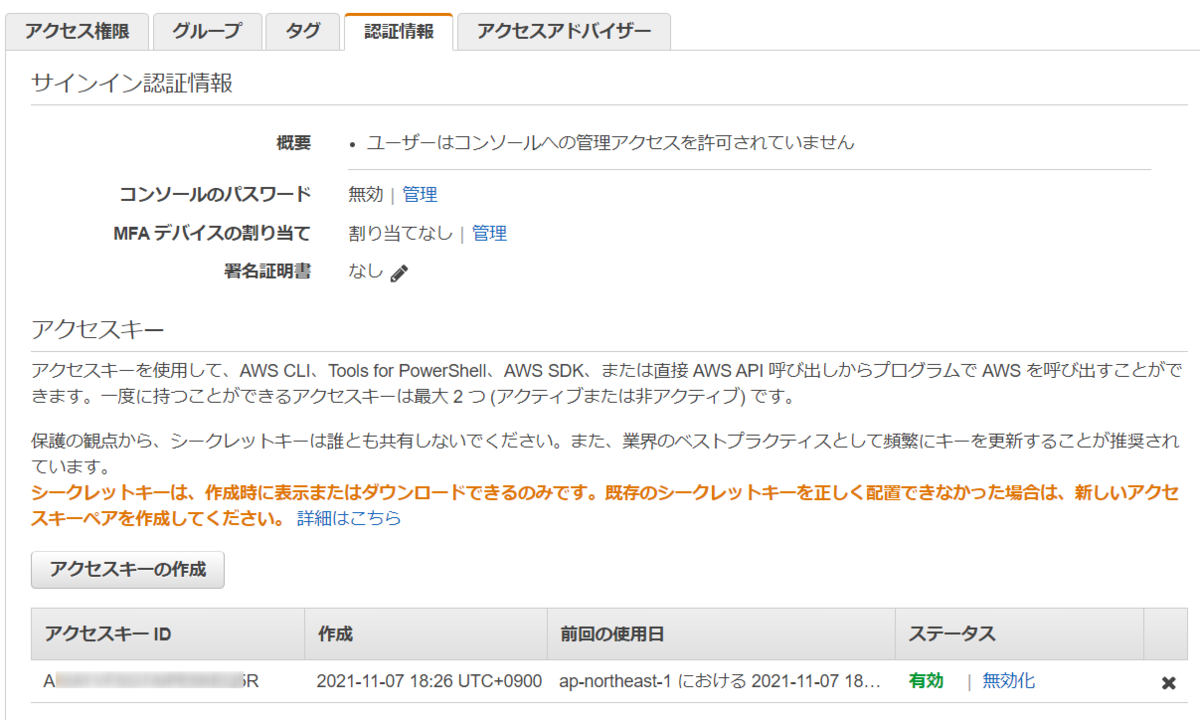
  3. IAMのアクセスキー、シークレットキーをメモする。
    • シークレットキーは作成時にしか確認できない。
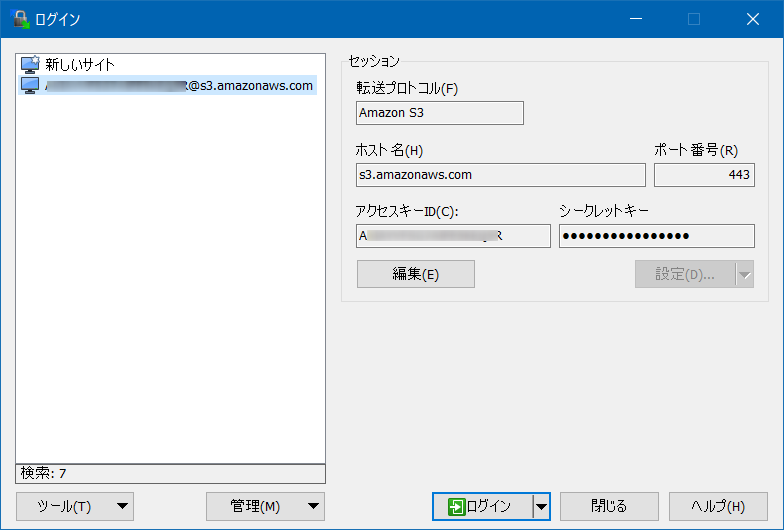
  4. WinSCPにアクセスキー、シークレットキーを入れる
参考にしたサイト

tech-blog.s-yoshiki.com off.tokyo

スクショのメモ

f:id:ebinafactory:20211107191351p:plain

f:id:ebinafactory:20211107191501p:plain

f:id:ebinafactory:20211107191910p:plain
IAMの認証情報

f:id:ebinafactory:20211107192242p:plain
WinSCPの設定画面